In many fields of technical, chemical or environmental regulation we use limit values. The purpose of establishing limit values in regulation is to set clear rules that protect safety of people, the environment and policy goals generally. This howtoregulate article analyses situations where there is a trade-off between different or inter-dependent parameters which are subject to limit values. Furthermore, we present a rational approach for deciding the trade-offs between limit values.

2. Firstly, lets consider the relatively simple situation involving two parameters. Where there are only two parameters, the introduction of a limit value for the first parameter does not always lead to a negative result for the other, second parameter. For example, the parameter of carbon dioxide (CO₂₎ emissions for diesel vehicles is aligned with the parameter for oxides of nitrogen (NO_X) emissions so that the introduction of a limit value for one also improves the results for the other parameter. However, such situations are rather rare. The introduction of a limit value for one parameter will usually be neutral for the second. However, sometimes the opposite is true, the limit value for one parameter triggers a negative result for another, requiring a decision about trade-offs. It is this latter situation that we wish to focus on when considering to introduce a limit value for a parameter, evidently we first should check whether there is really a trade-off with any other parameters. In some situations it might make sense to ask whether a requirement (containing a limit value) could be established that avoids a trade-off with another relevant parameter?

3. However, in the majority of situations, there is no leeway to amend the requirements in such a way that the trade-off is avoided. Hence we must decide where to put the trade-off? How to optimise between two, possibly inter-dependent parameters? To expand our earlier example of diesel vehicles to diesel and petrol vehicles. Petrol vehicles previously had higher fuel consumption, which caused higher CO₂ emissions, but lower emissions of the health damaging, and to some extent deadlier, NO_X. Regulators had to develop an approach for determining the best possible trade-off between optimising or reducing the two types of emissions.

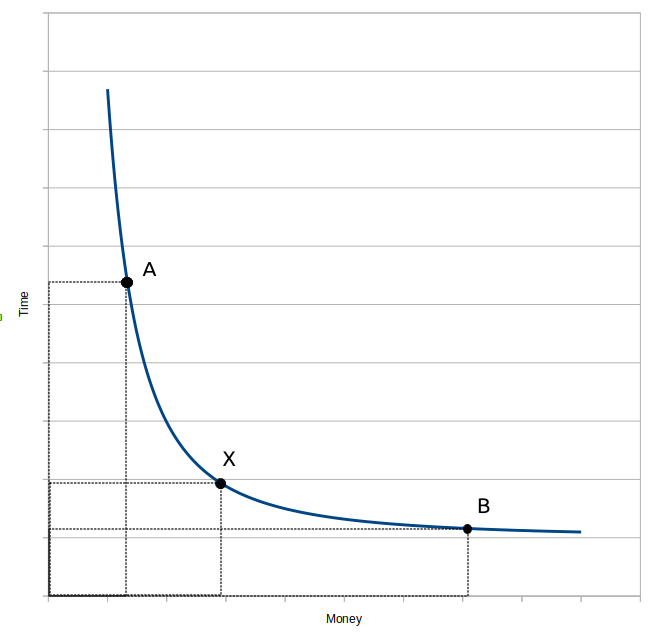
4. The trade-off the regulators had to consider between emissions of CO₂ and NO_X, is analogous to decisions that we all make in our day-to-day life when deciding between transport modes of travel. For example Diagram 1 represents a decision-making process about travel from city Y to city Z by bus (cheap, but slow, see point A of Diagram1), by plane (expensive, but fast, see point B) or by train (quite fast and still relatively cheap, here point X).

[Diagram 1.]

The curve represented can also be bent to the other side or be a straight line, subject to the situation.

5. The key to clear decision making visually represented at Diagram 1, between different transport modes, is the exchange rate between time and money. If a person believes that one hour is worth $40, s/he may decide differently to a person that believes one hour is worth only $10. But when the person has found the exchange rate, it can measure the “money” in units corresponding to one time unit. For example, one hour will be expressed by one centimetre on the vertical axis and one centimetre on the horizontal axis corresponds to $40. Thereby one can not only proceed with a clear mathematical calculation for the optimisation between time and money, but this will automatically already be expressed geometrically by the graph. In our example, the optimisation takes place slightly left from the point X, thus the train is the optimal mode of transport in terms of time and money. In more abstract terms: the best point on the curve is where the rectangle between the axes and the shortest lines linking the respective dot on the curve where the axes is smallest.

6. To develop an exchange rate between different parameters¹, one can apply different techniques as we illustrate again with the help of the transport example of before:

• Where policy decisions touch upon the interests of many people, whilst it is impossible to ask them all for their exchange rate, statistical methods can be used to obtain the relative best guess for the average subjective (hypothetical) exchange rate. With such methods, we might find out that the average subjective exchange rate between time and money is maybe $15 in one country and $23 in another. In absence of any better guess, regulators can take these average subjective values as a basis for determining the optimised trade-off in a certain jurisdiction.
• Both CO₂ and NO_X emissions cause deaths, though each have different causality chains. Thus deaths or, more precisely, lost life-years can become the common denominator which indirectly determines the exchange rate.
• Alternatively, money units can be chosen as a common denominator. Money as a common denominator has the advantage that simple economic effects can easily be taken into account, though the issue of fair distribution or equality remains problematic. The disadvantage is of course that everything needs to be monetised, even a life or life-year, suffering etc. Again a statistical method can be used to determine a “best-guess” or “average price”.
• Where both life-years or lives and money are at stake, there is no help: one has to define a price for a life or life-year. Again the price will depend on the respective jurisdiction. Strikingly, the value of a life (known as the value of a statistical life or VSL and value of a statistical life year or VSLY) is normally estimated at US$4.8 million² in the United States, in Australia AU$4.9 million³ whereas the VSL in Europe is much lower, at €1.5 million⁴.

7. All these approaches have a common goal: to compare apples and pears with a view to making relatively reasonable and relatively acceptable trade-off decisions. They are not ideal from the outset, but can be endlessly fine-tuned. Unfortunately, regulators have no choice: either they apply methods of the kind or they make their trade-off decisions instinctively which is, on average, worse.

8. Evidently, a precise mathematical calculation in accordance with the paragraphs above will not always be possible. However, it helps to keep the mathematical models in mind when developing pragmatic best guess approaches. We present below some approaches for pragmatic best guesses:

a) We can try to identify a zone where limit values for one parameter have almost never has any effect on the other, whilst the effect is very limited where any effect occurs.

b) We can try to identify a zone where limit values for one parameter almost never has any effect on the other, whilst the effect is not necessarily limited.

c) We can try to identify a zone where limit values for one parameter have an effect only in a minority of cases on the other, whilst the effect is very limited where any effect occurs.

d) We can try to identify a zone where limit values for one parameter have only in a minority of cases any effect on the other, whilst the effect is not necessarily very limited.

e) We can try to identify a zone where limit values for one parameter have an effect on the other, whilst the effect is very limited.

f) We can try to identify a zone where the trade-off is such that limit values for one parameter will never disproportionately harm the values of the other. In order to reach this goal, it might be necessary to set up precise requirements.

g) We can try to identify a zone where the trade-off is such that limit values for one parameter will on average not disproportionately harm the values of the other. In order to reach this goal, it might be necessary to set up precise requirements.

h) We can try to identify a zone where the trade-off is such that limit values for one parameter will on average not disproportionately harm the values of the other, but provide for the possibility to ask for an exemption where such is the case.

i) We can try to identify a zone where the trade-off is such that limit values for one parameter will on average not disproportionately harm the values of the other, but give the possibility to rebut the assumption that there is no disproportionate harm for the other; and if there is such disproportionate harm for the other, the limit value would be reduced / increased or completely devaluated.

How can the requirements, referred to at letters f) and g), change the trade-off between two goals?

9. Let us illustrate this with a real-life example. At least until 2015, there was a trade-off between the environmental goal of reducing the dissemination of mercury and the goal of optimised dental cure in cases where dental holes needed to be filled. Despite rare allergic reactions, dental amalgam (containing mercury) was regarded by dentists as the best possible filler in many situations. Despite many statements to the contrary in popular media, toxicity was found to be extremely low in virtually all of the more than 1000 studies about toxicity. Unlike most of the other fillers, dental amalgam does not shrink over time, which was important for dental care as shrinking triggered the risk for new caries. In fact, dental amalgam even expands and thus further reduces the risk of new caries forming. Dental amalgam containing mercury is more robust than other fillers. Still, there was a lot of debate between environmental policy defenders and those policy actors who had mainly dental health in mind. The debate could have been avoided by more regulatory awareness.

10. To optimise the trade-off between the two goals, environment and dental health, two types of requirements could have been set:

• Requirements for advanced placement techniques reducing the loss or emission of mercury at the time of placement: These requirements could reduce the negative effects on the environment and thus shift the trade-off.
• Requirements requesting other fillers not to shrink or even to expand: These requirements reduce the comparative advantage of dental amalgam when compared to other fillers so that the environmental considerations can more easily prevail. This type of requirement, touching alternatives and thus even not the problematic product/item, is often not spotted, though being equally effective.

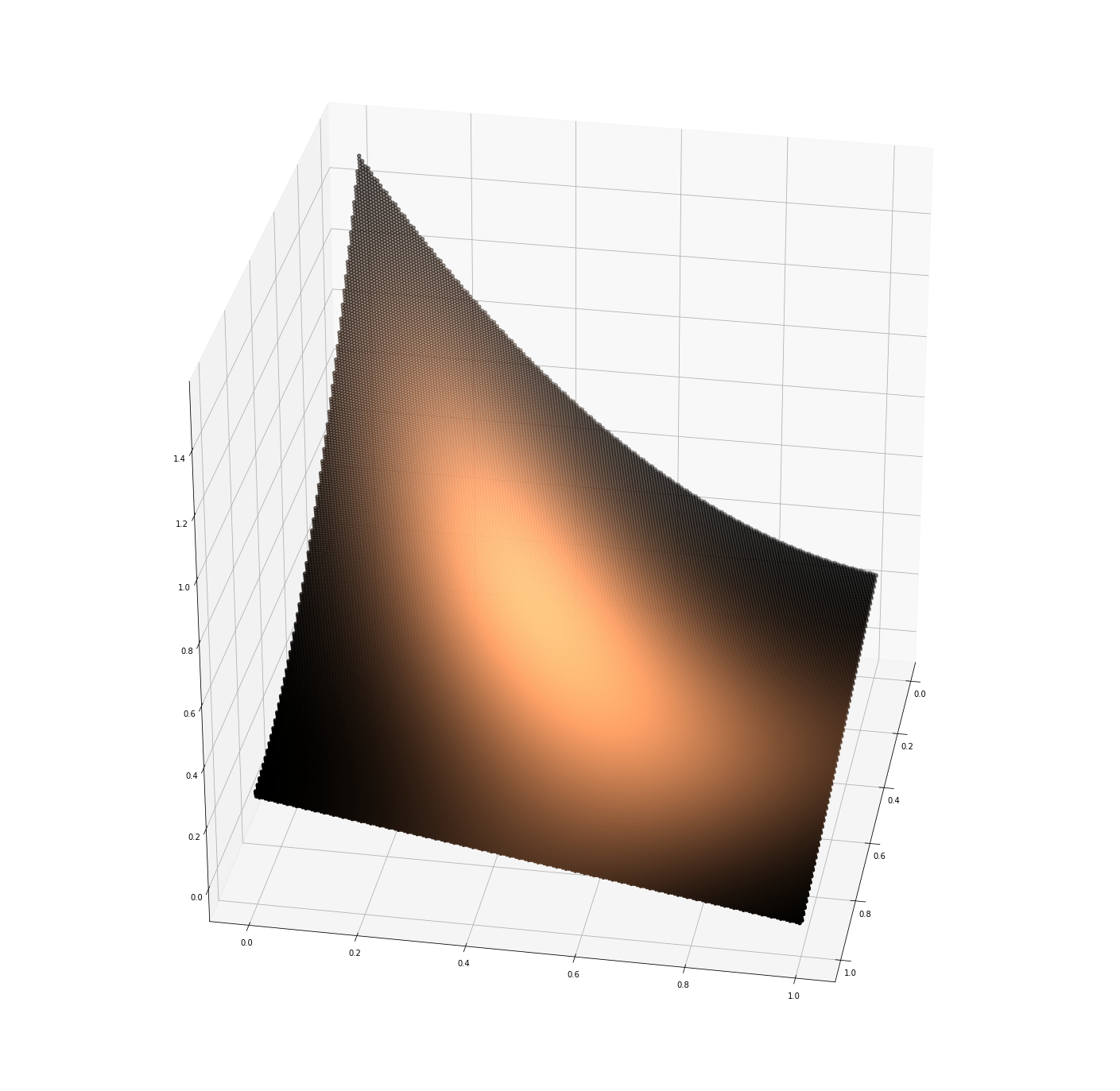
11. So far, we have only dealt with trade-offs between two goals. How about situations where three parameters are inter-dependent? In terms of mathematical model, we need to expand the graph at Diagram 1, to include a third axis, e.g. aiming at measuring “discomfort of travel” borrowing our earlier example about different modes of transport. The two-dimensional curve at Diagram 1 becomes a bent surface which can only be represented in a three-dimensional way (see Diagram 2). All the points on the bent surface (the yellow coloured middle part) express trade-offs for the three parameters time, money and discomfort.

[Diagram 2.]

12. A precise preference structure is already difficult to establish for one single person. Already for one person, this would require a multitude of questions and answers covering a high number of alternative situations to be considered. More difficult still, is estimating the (average) trade-off bent surface for a multitude of persons is tricky. It would require sophisticated statistical methods that regulators mostly do not use. Still, it might be helpful to have a clear mathematical illustration to guide us and the clearest we found is the bent surface at Diagram 2.

13. Regulators should aim to avoid making any trade-off decisions between different parameters which are subject to limit values, by instinct. We present a rational approach for deciding any trade-offs between limit values using mathematical models in two-dimensional form (for two parameters) and in three-dimensional form (for three parameters). Such a decision-making approach is transparent, introduces rigour where instinct was previously used and enables the regulator to decide how to approach the task of optimisation.

Written by Manfred Kohler